Introduction
Dans une note de blog précédente, nous présentions les fondements théoriques de l’embedding de mots. Ici, nous présenterons comment un modeste modèle de ce type peut suffire à construire un outil capable de jouer à une variante du célèbre jeu de société Code Names : Podwords.
Motivation
Le but n’est pas un concours de la plus grosse IA. Au contraire, on cherche ici à voir jusqu'où on peut aller dans la complexité de tâche adressée, avec l'outil le plus minimaliste possible. En somme, faire le maximum avec le minimum. Jouer à une sorte de Code Names, sans jeu de données de parties jouées, sans réseau de neurones complexe, mais avec un simple jeu d’embedding de mots courants.
Modèle d’embedding
Définition
Pour les intéressés, les fondamentaux mathématiques sont consultables dans notre note de blog précédente.
Ici, le parti-pris est de présenter très simplement les choses, en se contentant de donner l’intuition.
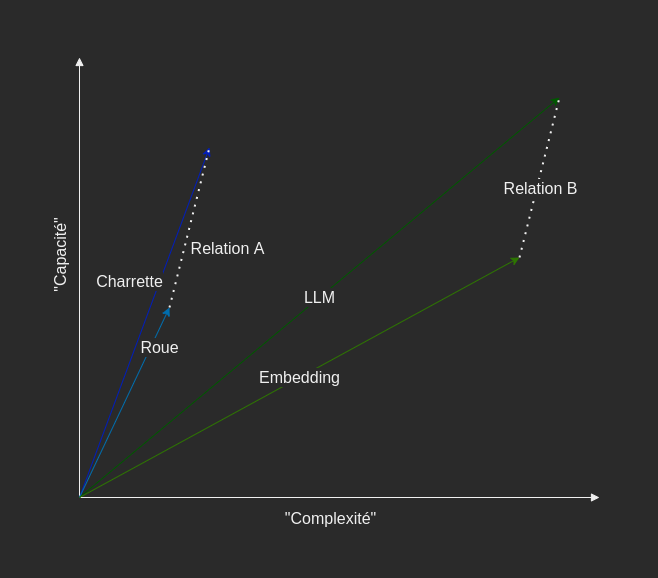
Prenons l’analogie suivante : « L’embedding est aux LLM, ce qu’est la roue à une charrette ».
Ceci est loin de donner une définition satisfaisante de l’embedding. Cependant, elle permet de se représenter les choses.
Il y a une relation entre l’embedding et les LLM.
Il y a une relation entre une roue et une charrette. Ces relations sont similaires.
Schématiquement, ces relations sont des vecteurs et ces deux vecteurs sont égaux.
Mais comment décrire cette relation ? On peut identifier des composants au vecteur de la relation :
- « est un composant de »
- « a été inventé avant »
- « est plus simple que »
- « a moins de capacité que »
Eh bien, choisir un modèle d’embedding, c'est-à-dire un outil qui donne la représentation vectorielle d’un mot, c’est choisir un certain nombre de composants structurant l’espace des mots pour rendre compte de relations entre eux. Évidement, comme on veut aussi pouvoir se représenter des tas d’autres mots, typiquement de l’ordre de 90 000 pour le français, il va falloir plus de dimensions à notre espace. Cependant, l’idée est là, ne pas avoir une dimension par mot (comme c’est le cas pour un encodage one-hot, mais trouver les bonnes composantes pour réduire le nombre de dimensions, tout en rendant compte de manière satisfaisante de l’ensemble des relations existantes entre les mots. La valeur de l’embedding réside dans les relations linéaires entre vecteurs que sous-tend la structuration de l’espace choisi. Passer à cet espace vectoriel structuré permet le calcul de distance, la projection, voire une arithmétique d’addition, de soustraction, voire de moyennation des vecteurs d’embedding, et donc des mots. Ici, on restera simple et on se contentera de calculer la similitude entre deux mots, par le calcul du cosinus de leurs vecteurs d’embedding.
Modèle d’embedding utilisé
Il est naturel que différentes structurations de l’espace des mots soient possibles et donc que différents modèles d’embedding puissent coexister.
Ces derniers ont des caractéristiques et des performances variables suivant la tâche adressée.
Dans la perspective minimaliste de ce démonstrateur, nous optons pour Word2Vec.
Notons que ce n’est pas le modèle qui est utilisé mais le résultat de la modélisation, i.e. une liste de paires : mot et sa représentation vectorielle.
Les embeddings utilisés sont fournis par Jean-Philippe Fauconnier, sous la référence frWac_non_lem_no_postag_no_phrase_200_cbow_cut100 (sous licence CC-BY 3.0).
Ils sont obtenus par l’approche cbow (cf. la note de blog ou le papier académique pour plus de détails),
sur le corpus FrWac corpus.
Construit en 2008, il est bâti sur un corpus de 1,6 milliard de mots, à partir du Web en limitant l'exploration au domaine .fr. Les vecteurs sont de dimension 200.
Il est important de noter que ces dimensions ne sont pas des concepts explicites comme l’exemple précédent, mais des notions « machines » basées sur des fréquences d’apparitions.
Par ailleurs, pour améliorer l’expérience de jeu, certains mots ont été écartés du corpus.
Il s’agit de mots trop fréquents, de mots trop méconnus ou encore injurieux (ex: « de », « agélaste », …).
Générer des indices
C’est entendu, l’idée ici sera de créer un programme capable de proposer des mots indices dans une partie de Podwords, en partant uniquement d’un set de vecteurs d’embedding pour les mots les plus fréquents de la langue française.
Voyons comment faire cela simplement.
On passera sur certaines fonctionnalités simples du moteur de jeu, comme déterminer lorsqu'une partie est gagnée ou perdue par exemple, pour se concentrer sur la tâche qui nous intéresse ici : comment, à partir de l’information sur l’état du jeu, formuler une proposition d’indice ?
Une proposition d’indice se compose de deux éléments :
- un mot indice - qui ne doit pas être de la même famille qu’un des mots encore non désigné sur la grille
- un nombre de mots ciblés - qui est une indication au joueur sur le nombre de mots ciblés qu’il devrait pouvoir pointer avec ce mot indice
On peut décomposer le processus de génération en deux étapes.
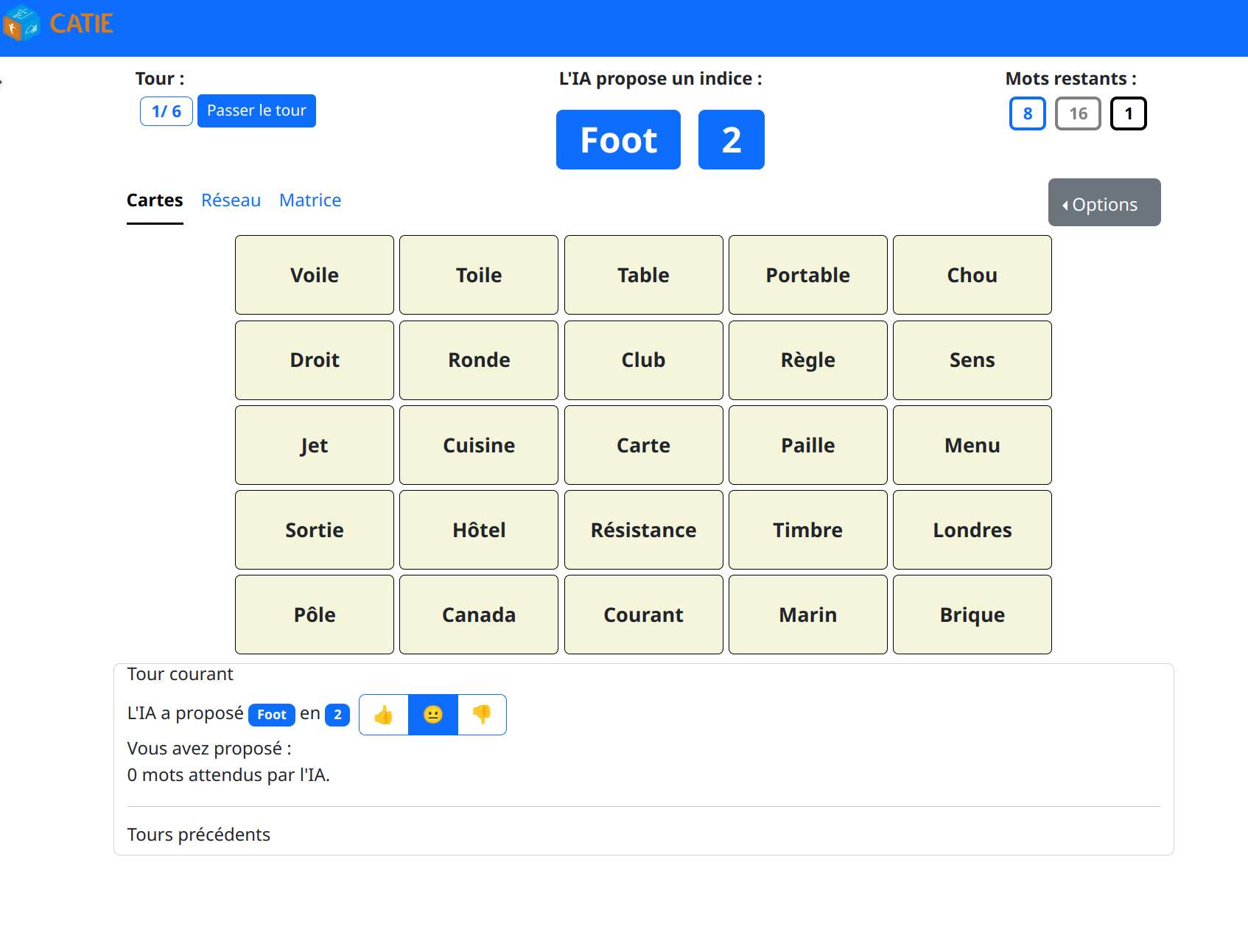
On dispose à ce stade de l’état de la grille. On peut alors écarter les mots déjà pointés par l’utilisateur, qui ne sont plus « actifs ».
A noter, pour les autres mots, le programme « sait » s’ils sont à faire deviner, neutres ou tabous.
En résumé, les étapes sont les suivantes (on va détailler cela ci-dessous) :
1) créer la liste de tous les groupes de mots cibles possibles
2) pour chaque groupe
2.1) obtenir une liste de n mots indices candidats
2.2) affiner le calcul du score des mots indices candidats, pour selectionner le meilleur
3) pour chaque taille de groupe, déterminer la meilleure proposition (paire indice:groupe_mots_cibles)
4) sélectionner parmis les propositions ayant une score de facilité suffisant, la proposition du plus grand groupe de mots cibles.
Étape 1 : elle consiste à lister l’ensemble des combinaisons possibles de groupes de mots à faire deviner (sans répétition, ni ordre).
On considère ainsi tous les groupes possibles de 1 mot parmi les n, de 2 mots, etc. jusqu’au seul groupe possible de n mots.
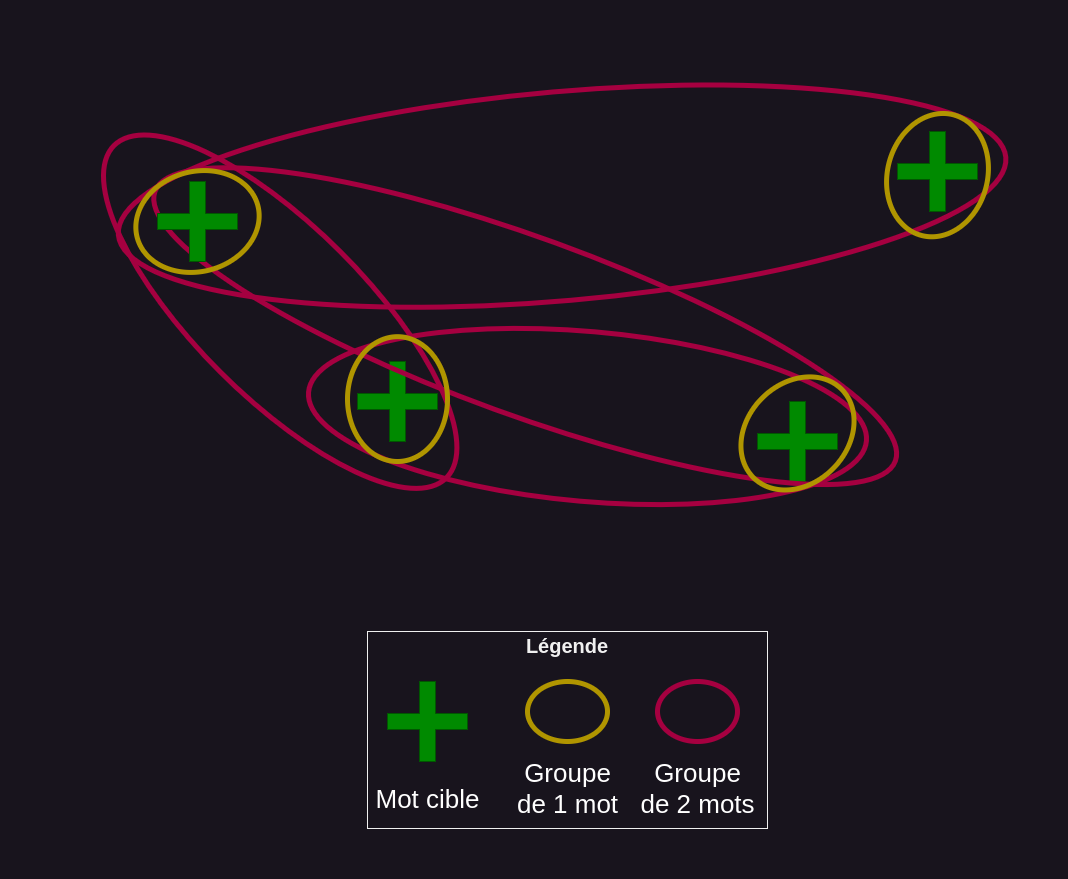
Étape 2.1 : elle fournit, pour chaque groupe, une liste de n mots indices candidats.
Ces mots sont ceux qui sont à la fois le plus proche possible des mots cible et le plus loin des mots tabous (oui, à ce stade, on ignore les mots neutres).
Pour ce faire, le barycentre de l’ensemble des vecteurs d’embedding des mots est calculé, avec une pondération positive pour les mots cibles et une pondération négative pour les mots tabous.
Les n mots indices candidats les plus proches de ce barycentre sont alors retournés.
Cette approximation peut potentiellement dégrader la qualité des indices générés.
Mais elle vise à restreindre le nombre de mots indices candidats qui seront passés à l’étape suivante.
Sans considération pour le coup de calcul, on pourrait ignorer cette étape et passer l’ensemble des mots du corpus à l’étape suivante.
En outre, à cette étape, on détermine pour chacun des n mots indices candidats s’il est valide.
Il est invalide s’il est de la même famille lexicale qu’un des mots de la grille non encore découverts.
Pour cacher la poussière sous le tapis, on prétendra ici qu’il s’agit d’une trivialité.
Même si en réalité, la solution déployée a des ratés, elle laisse passer des indices invalides.
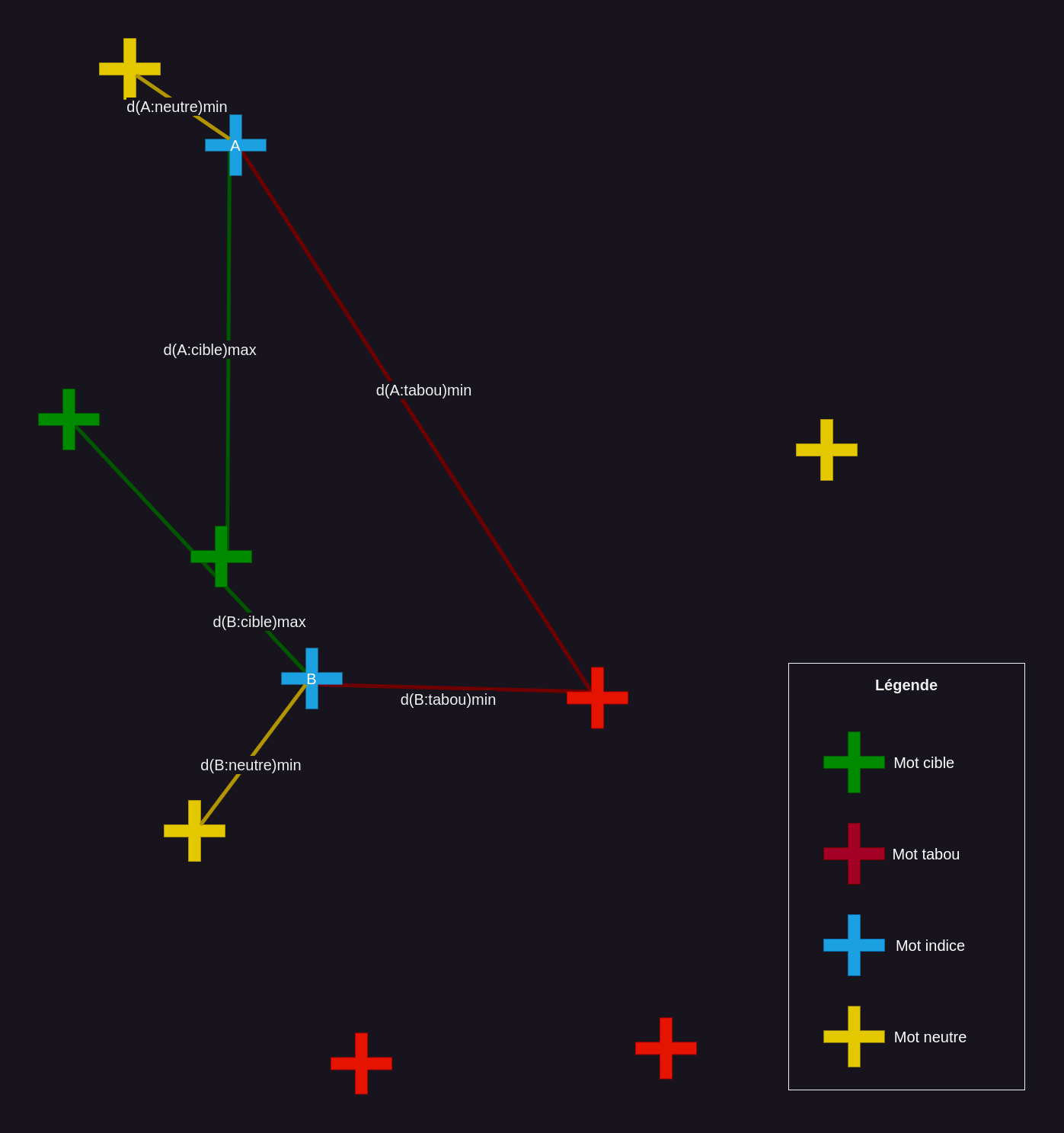
Étape 2.2 : elle consiste à affiner le calcul pour chacun des n mots retournés par la précédente étape, pour déterminer le mot indice le plus adapté pour chaque groupe de mots cibles.
Ainsi, pour chaque groupe de mots cibles, et pour chacun de ses mots indices candidat, on :
- mesure la proximité maximale entre le mot indice et chacun des mots tabous d’une part ainsi que chacun des mots neutres d’autre part. On cherche ici à mesurer « le pire cas », c’est pourquoi on retient la similarité la plus forte (i.e. la distance la plus faible) pour chacune des deux catégories.
- fait la somme pondérée des deux proximités obtenues, avec un poids pour les mots tabous cinq fois supérieur à celui des mots neutres. En effet, il est plus gênant d’être proche d’un mot tabou, qui entraîne instantanément la fin de partie, que d’un mot neutre qui ne fait que terminer le tour.
- mesure la proximité la plus faible entre le mot indice et chacun des mots cibles. Là encore, on recherche le cas le plus défavorable.
- calcule le ratio entre deux quantités, la proximité minimale vis-à-vis d’un mot cible, sur la proximité maximale d’un mot non ciblé (cf. la somme précédente).
- normalise le ratio pour passer d’une valeur définie entre [-1, 1], vers un score défini sur l’intervalle [0, 1].
Ce score représente la « facilité », plus ce score est élevé, plus le mot indice permet à l’utilisateur de trouver facilement les mots cibles du groupe.
Étape 3 : pour chaque taille de groupe (1 mot, 2 mots…), on ne garde alors que la proposition ayant le score de facilité le plus élevé.
Soit deux groupes A et B de même taille n. Si le score de facilité de A est supérieur au score de B, alors pour la taille de groupe n, c’est la proposition A (et son mot indice correspondant) qui sera retenue.
Étape 4 : à l’issue de l’étape précédente, on dispose donc d’une liste de groupes de mots cibles, un par taille, et pour chacun le meilleur mot indice, avec son score de facilité.
Toujours dans une approche minimaliste, deux conditions complémentaires sont utilisées.
La proposition retenue sera celle ayant le plus grand score de facilité, sauf si des propositions ont un score supérieur à un certain seuil, auquel cas c’est la proposition correspondant au plus grand groupe de mots cibles qui sera sélectionnée.
En effet, parvenir à faire deviner en un tour 3 mots cibles a plus de valeur que de faire deviner 1 mot cible.
Avec cette mécanique simple, le programme parvient globalement à formuler des propositions cohérentes pour un utilisateur humain. Les performances n’ont pas été mesurées en conditions rigoureuses. Nos expérimentations informelles semblent toutefois indiquer que la machine permet un taux de victoire de l’utilisateur analogue à celui obtenu lorsque c’est un humain relativement débutant à ce jeu qui génère des indices.
Comprendre les propositions de l’algorithme
Que ce soit avec un humain ou une machine, lorsqu'on joue à Code Names, une question revient régulièrement « mais pourquoi ce choix d’indice ? ». Dans le cas présent, le mécanisme de génération des indices en lui-même est simple. Ce qui est difficile est l’appréhension de la représentation des mots que se fait la machine. Ici les notions d’explicabilité et d’interprétabilité se chevauchent. Pour rendre plus compréhensible une proposition, il faudrait donc pouvoir représenter l’espace des vecteurs d’embedding qu’utilise la machine, soit un espace à 200 dimensions. Quand on voit la tête d’un carré lorsqu'il passe en dimension 4, on pressent que cela ne peut pas se faire directement. Du moins si l’on vise à rendre les choses plus explicites pour un esprit humain. Il faut trouver un moyen de synthétiser l’information pour qu’elle soit accessible à un esprit qui se contente de caboter en 3 voire 4 dimensions. Deux fonctionnalités ont été développées pour ce faire. Notons que ces outils sont cohérents avec la démarche d’exploration de l’embedding. Mais ces fonctionnalités sont orthogonales à l’aspect ludique de Podwords. En cherchant « à comprendre la machine » quand elle joue à nous faire deviner, on accède à des informations qui doivent être ignorées pour qu’il y ait jeu, comme la catégorie cachée de chaque mot sur la grille.
Matrice de distance
La vue « Matrice » affiche la distance pour chacune des paires de mots que l'on peut constituer (avec les mots non révélés de la grille plus l'indice). Chaque ligne et chaque colonne représentent un mot. L'intersection des deux lignes donne la distance entre les deux mots. La coloration bleue à noire indique une distance faible, tandis que l'orange indique une distance élevée. En somme, cette représentation compresse l’information issue de l’espace d’embedding pour ne garder qu’une valeur, un score (tiré du calcul de similarité entre les vecteurs par le calcul du cosinus), sans dimension, facilement assimilable par l’esprit humain.
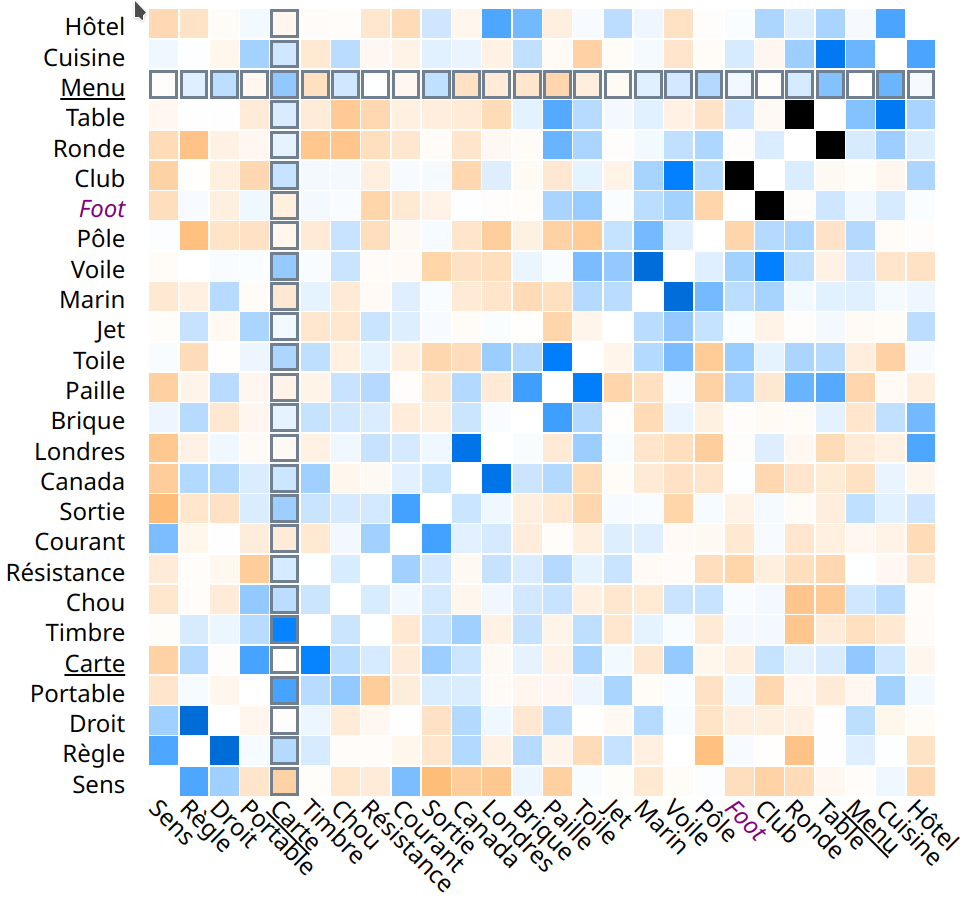
De plus, l'ordre des mots sur chaque axe est arrangé de manière à mieux faire ressortir les zones de paires ayant une forte ou une faible distance. Pour ce faire, on détermine l’ordre des mots par un algorithme d’optimisation de l'ordonnancement linéaire des feuilles des arbres générés par le regroupement hiérarchique (en somme, on cherche à optimiser la manière de représenter un dendrogramme).
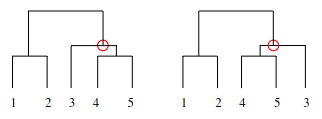
Graphe du réseau de mots
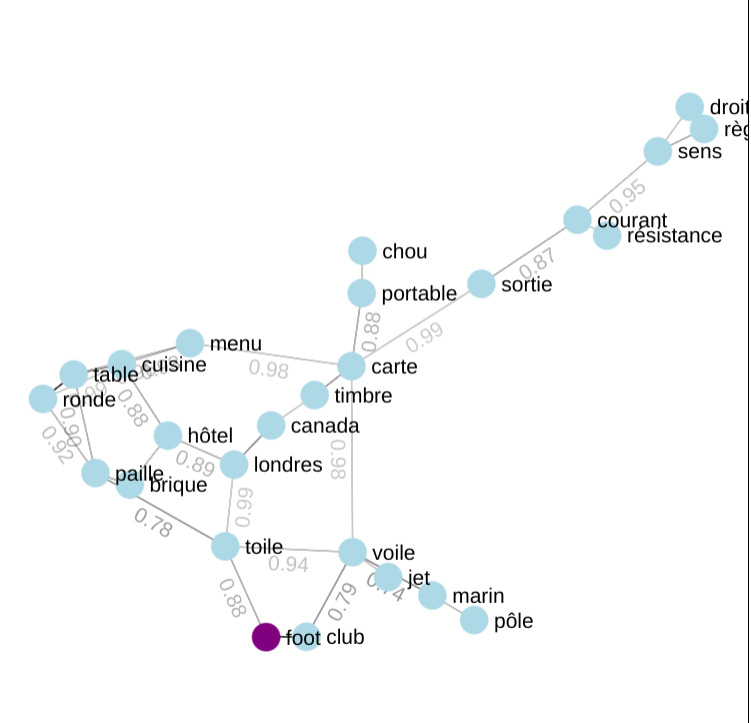
Là encore, l’idée centrale est de proposer une représentation simplifiée des mots de la grille dans l’espace d’embedding. La vue « Réseau » affiche l'indice et l'ensemble des mots non révélés de la grille par une représentation en 2D des relations entre eux. A noter, il ne s’agit pas à proprement parler d’une projection de l’espace 200D de l'embedding vers un espace 2D. Ici un plus grand degré de liberté est pris pour réaliser le dessin. L’assignation des positions des nœuds et arrêtes sont est rapport avec la position dans l’espace d’embedding, comme pour la matrice. Seule l’information de « similitude » entre paires de mots est exploitée. Un seuil de distance est choisi, de manière à garantir la connexité du graphe (c'est-à-dire qu'il n'y ait pas de groupes de mots détachés du reste). Toutes les paires de mots plus proches entre elles que ce seuil, sont reliées par des arêtes. Cette représentation est réalisée avec Sigma JS et plus précisément l’algorithme ForceAtlas2. Lorsque deux mots sont considérés comme proches (seuillage), ils sont reliés par un trait (mais ne sont pas forcément affichés à côté l'un de l'autre). Ainsi, certains mots peuvent n'être reliés qu'à peu d'autres mots, tandis que certains autres mots sont liés à beaucoup d'autres mots. La valeur numérique affichée est la distance entre les mots. Afin de permettre à l’utilisateur d’explorer cette représentation de l’espace, la vue est interactive : on peut zoomer, se déplacer sur les côtés et même cliquer sur un mot pour ne voir que lui ainsi que ses voisins directs. L’utilisateur peut par ailleurs compléter l’affichage par l’ajout d’informations sur la catégorie des mots du graphe.
Conclusion
Et voila, nous obtenons ainsi Podwords.
Ce démonstrateur réussit à montrer qu’avec un mécanisme relativement simple, on peut aller assez loin dans une apparence « d’intelligence ». Ici un simple jeu de vecteurs d’embedding pour des mots courants parvient à adresser une tâche considérée comme difficile par les humains, fournir des indices à Code Names.
De plus, ses fonctionnalités annexes d’explicabilité permettent à l’utilisateur d’explorer, à travers une projection 2D, comment les mots de la grille sont positionnés dans l’espace d’embedding. C'est-à-dire une représentation de l'univers des mots et des relations qu'ils ont entre eux. Ceci détaille le mécanisme sous-jacent de création des indices.
Et la dernière gageure est que tout ceci est obtenu au travers d'un objet ludique. Nous espérons que vous aurez autant de plaisir à jouer à Podwords que nous en avons eu à le développer.
Alors pourquoi s’arrêter en si bon chemin ? Comme indiqué dans les encarts précédents, différentes améliorations pourraient prolonger ces travaux. N’hésitez pas à voter pour nous indiquer quelle suite vous voudriez voir donnée :
- 💡 Faites des Schtroumpfs ! ⇒ Permettre de jouer avec différents modèles d’embedding et voir comment ils sont plus ou moins adaptés à la tâche. Par là même, explorer ce qui pourrait émerger de l’utilisation de modèles d’embedding moins génériques. Peut-on réussir à faire emerger des profils ?
- 💡 Ajoutez une boite de vitesse ! ⇒ Affiner la méthode de sélection de la proposition d’indice retenue, notamment pour permettre de combiner le score de facilité et celui de gain relatif, en tenant compte de l’avancement de la partie. Est-ce qu’ajouter cette petite complexité augmente sensiblement les performances ?
- 💡 Expliquez nous ça ! ⇒ Enrichir l’explicitation des éléments ayant conduit à la formulation d’un indice. Peut-on rendre plus explicite l’importance de chaque mot de la grille sur l’indice généré, y compris celle des mots tabou et neutres ?
Et pourquoi pas, passer un jour à une variante plus coriace, impliquant la multimodalité : Code Names Image !